Network Data Analysis Group

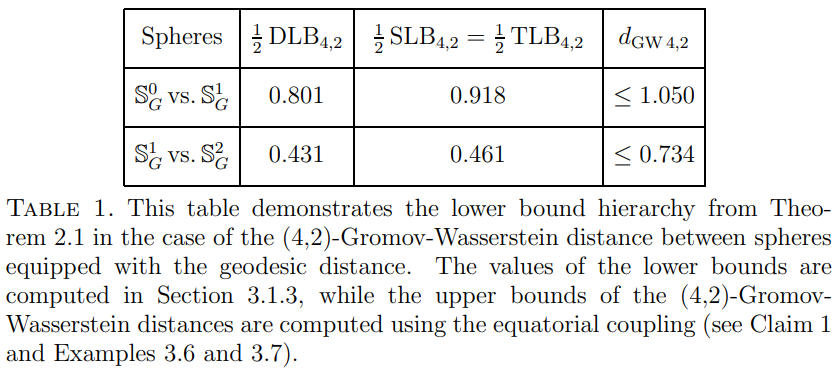
The Gromov-Wasserstein distance between spheres
In this paper we consider a two-parameter family {dGWp,q} of Gromov-Wasserstein distances between metric measure spaces. By exploiting a suitable interaction between specific values of the parameters p and q and the metric of the underlying spaces, we determine the exact value of the distance dGW4,2 between all pairs of unit spheres of different dimension endowed with their Euclidean distance and their uniform measure. See [Arya, Auddy, Edmonds, Lim, Mémoli and Packer, 2023] for our work.

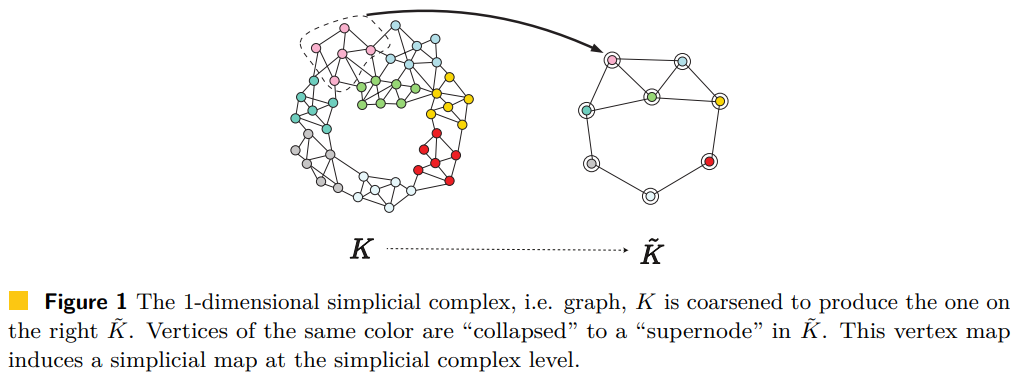
A Generalization of the Persistent Laplacian to Simplicial Maps
The (combinatorial) graph Laplacian is a fundamental object in the analysis of, and optimization on, graphs. Via a topological view, this operator can be extended to a simplicial complex K and therefore offers a way to perform "signal processing" on p-(co)chains of K. Recently, the concept of persistent Laplacian was proposed and studied for a pair of simplicial complexes K ↪ L connected by an inclusion relation, further broadening the use of Laplace-based operators. In this paper, we significantly expand the scope of the persistent Laplacian by generalizing it to a pair of weighted simplicial complexes connected by a weight preserving simplicial map f: K → L. Such a simplicial map setting arises frequently, e.g., when relating a coarsened simplicial representation with an original representation, or the case when the two simplicial complexes are spanned by different point sets, i.e. cases in which it does not hold that K ⊂ L. However, the simplicial map setting is much more challenging than the inclusion setting since the underlying algebraic structure is much more complicated. We present a natural generalization of the persistent Laplacian to the simplicial setting. To shed insight on the structure behind it, as well as to develop an algorithm to compute it, we exploit the relationship between the persistent Laplacian and the Schur complement of a matrix. A critical step is to view the Schur complement as a functorial way of restricting a self-adjoint positive semi-definite operator to a given subspace. As a consequence of this relation, we prove that the qth persistent Betti number of the simplicial map f: K → L equals the nullity of the qth persistent Laplacian Δ_q^{K,L}. We then propose an algorithm for finding the matrix representation of Δ_q^{K,L} which in turn yields a fundamentally different algorithm for computing the qth persistent Betti number of a simplicial map. Finally, we study the persistent Laplacian on simplicial towers under weight-preserving simplicial maps and establish monotonicity results for their eigenvalues. See [Gülen, Mémoli, Wan and Wang, 2023] for our work.

Ephemeral Persistence Features and the Stability of Filtered Chain Complexes
We strengthen the usual stability theorem for Vietoris-Rips (VR) persistent homology of finite metric spaces by building upon constructions due to Usher and Zhang in the context of filtered chain complexes. The information present at the level of filtered chain complexes includes ephemeral points, i.e. points with zero persistence, which provide additional information to that present at homology level. The resulting invariant, called verbose barcode, which has a stronger discriminating power than the usual barcode, is proved to be stable under certain metrics which are sensitive to these ephemeral points. In some situations, we provide ways to compute such metrics between verbose barcodes. We also exhibit several examples of finite metric spaces with identical (standard) VR barcodes yet with different verbose VR barcodes thus confirming that these ephemeral points strengthen the discriminating power of the standard VR barcode. See [Mémoli and Zhou, 2023] for our work.

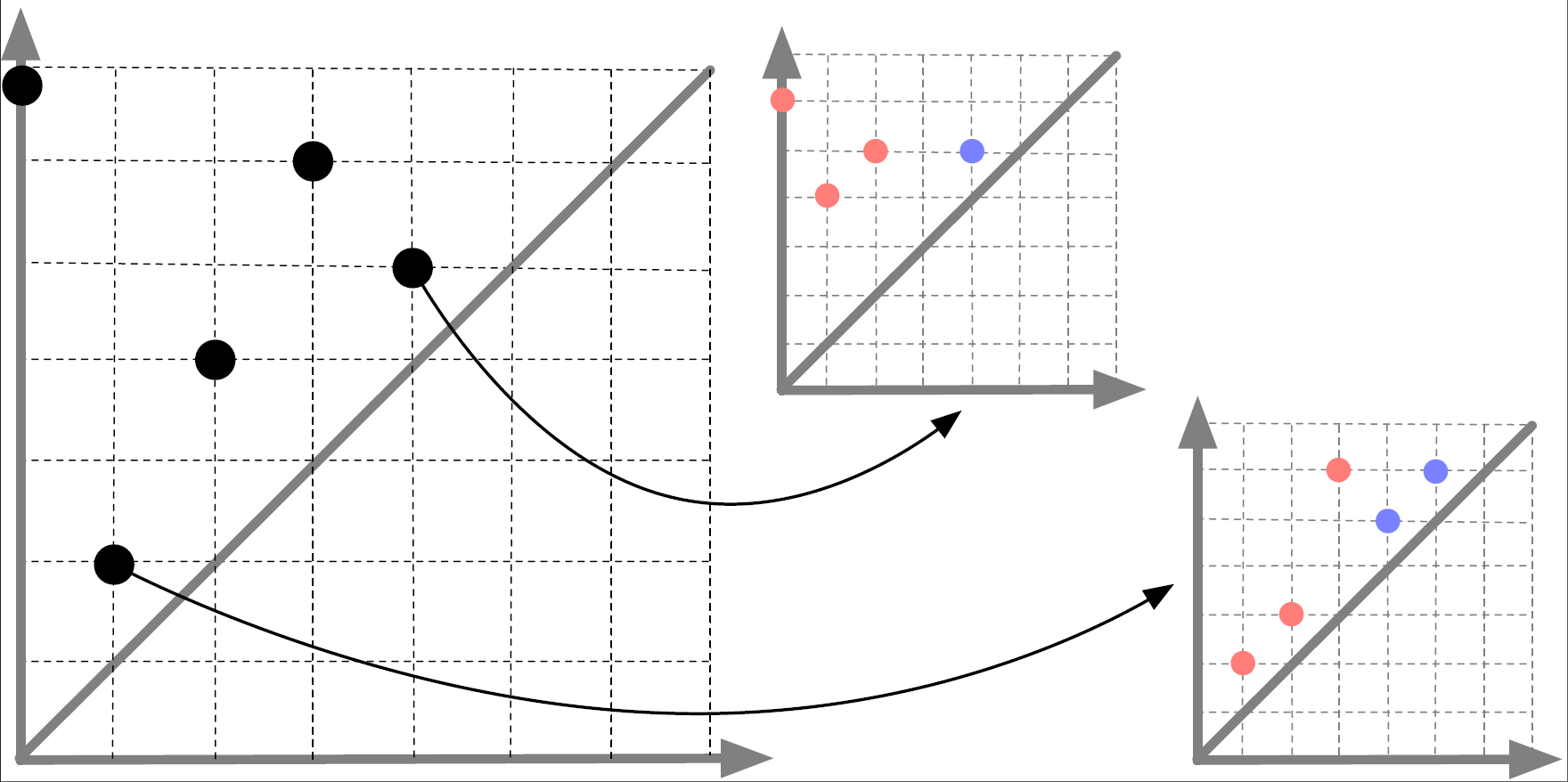
Meta-Diagrams for 2-Parameter Persistence
We first introduce the notion of meta-rank for a 2-parameter persistence module, an invariant that captures the information behind images of morphisms between 1D slices of the module. We then define the meta-diagram of a 2-parameter persistence module to be the Möbius inversion of the meta-rank, resulting in a function that takes values from signed 1-parameter persistence modules. We show that the meta-rank and meta-diagram contain information equivalent to the rank invariant and the signed barcode. This equivalence leads to computational benefits, as we introduce an algorithm for computing the meta-rank and meta-diagram of a 2-parameter module M indexed by a bifiltration of n simplices in O(n³) time. This implies an improvement upon the existing algorithm for computing the signed barcode, which has O(n⁴) time complexity. This also allows us to improve the existing upper bound on the number of rectangles in the rank decomposition of M from O(n⁴) to O(n³). In addition, we define notions of erosion distance between meta-ranks and between meta-diagrams, and show that under these distances, meta-ranks and meta-diagrams are stable with respect to the interleaving distance. Lastly, the meta-diagram can be visualized in an intuitive fashion as a persistence diagram of diagrams, which generalizes the well-understood persistence diagram in the 1-parameter setting. See [Clause, Dey, Mémoli and Wang, 2023] for our work.

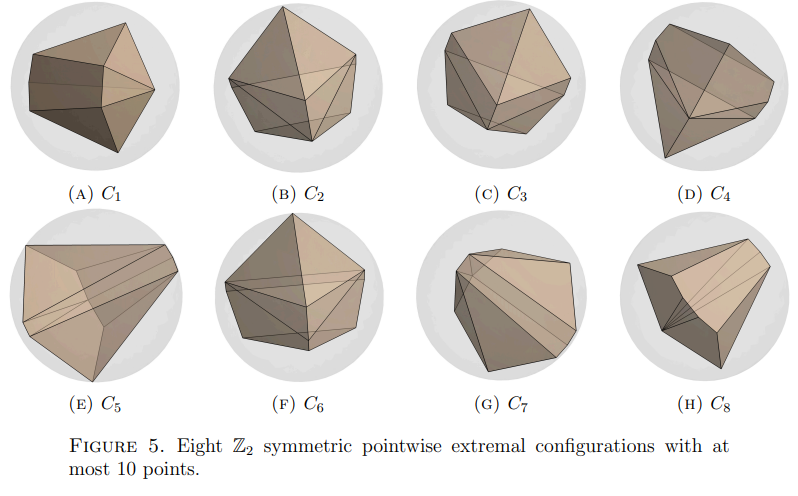
EXTREMAL SPHERICAL POLYTOPES AND BORSUK’S CONJECTURE
We generate anti-self-polar polytopes via a numerical implementation of the gradient flow induced by the diameter functional on the space of all finite subsets of the sphere, and prove related results on the critical points of the diameter functional as well as results about the combinatorics of such polytopes. We also discuss potential connections to Borsuk’s conjecture. See [Katz, Mémoli and Wang, 2023] for our work.

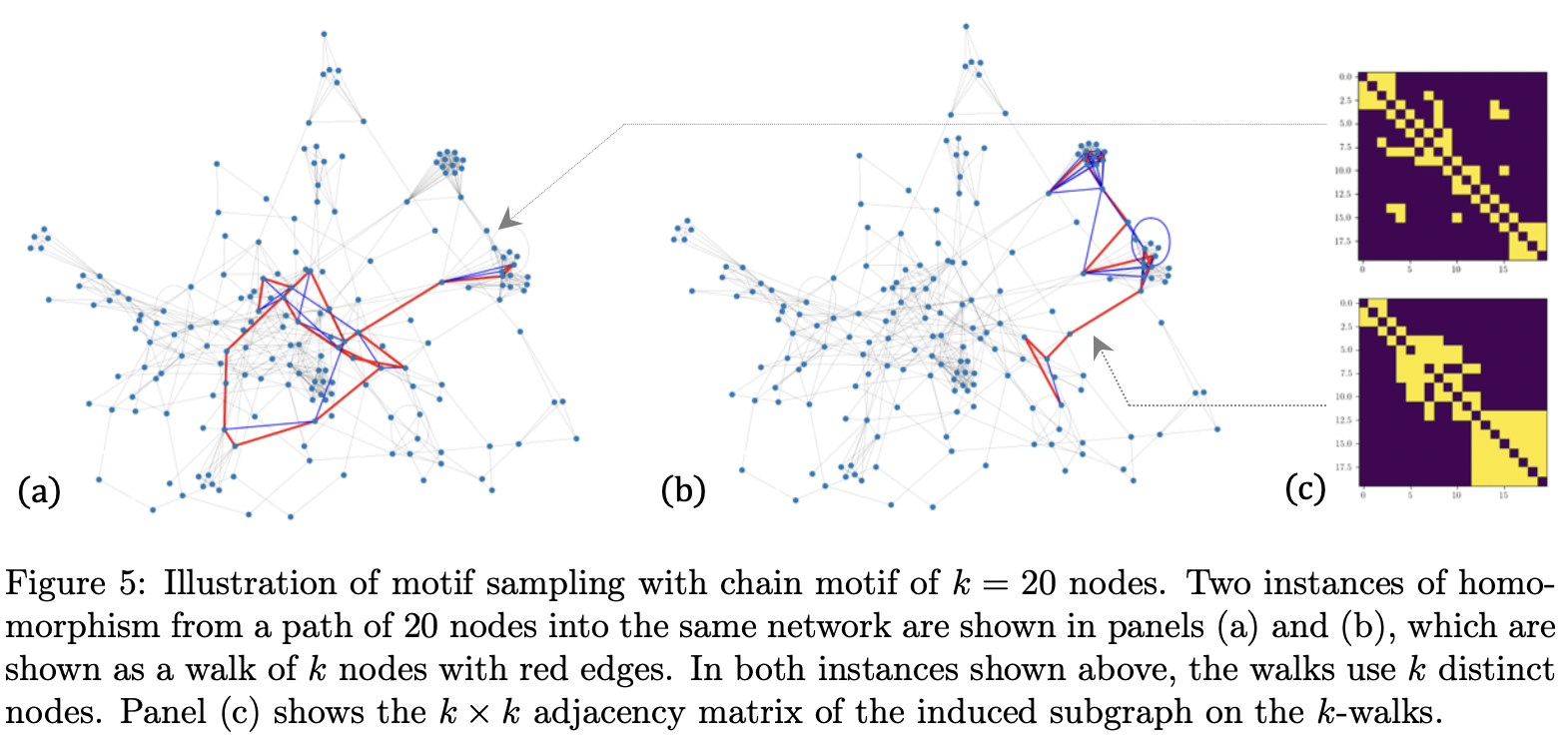
Sampling random graph homomorphisms and applications to network data analysis
A graph homomorphism is a map between two graphs that preserves adjacency relations. We consider the problem of sampling a random graph homomorphism from a graph into a large network. We propose two complementary MCMC algorithms for sampling random graph homomorphisms and establish bounds on their mixing times and the concentration of their time averages. Based on our sampling algorithms, we propose a novel framework for network data analysis that circumvents some of the drawbacks in methods based on independent and neighborhood sampling. Various time averages of the MCMC trajectory give us various computable observables, including well-known ones such as homomorphism density and average clustering coefficient and their generalizations. Furthermore, we show that these network observables are stable with respect to a suitably renormalized cut distance between networks. We provide various examples and simulations demonstrating our framework through synthetic networks. We also demonstrate the performance of our framework on the tasks of network clustering and subgraph classification on the Facebook100 dataset and on Word Adjacency Networks of a set of classic novels. See [Lyu, Mémoli and Sivakoff, 2023] for our work.

Persistent Cup Product Structures and Related Invariants
One-dimensional persistent homology is arguably the most important and heavily used computational tool in topological data analysis. Additional information can be extracted from datasets by studying multi-dimensional persistence modules and by utilizing cohomological ideas, e.g. the cohomological cup product. In this work, given a single parameter filtration, we investigate a certain 2-dimensional persistence module structure associated with persistent cohomology, where one parameter is the cup-length \(\ell\geq 0\) and the other is the filtration parameter. This new persistence structure, called the persistent cup module, is induced by the cohomological cup product and adapted to the persistence setting. Furthermore, we show that this persistence structure is stable. By fixing the cup-length parameter \(\ell\), we obtain a 1-dimensional persistence module, called the persistent \(\ell\)-cup module, and again show it is stable in the interleaving distance sense, and study their associated generalized persistence diagrams. In addition, we consider a generalized notion of a persistent invariant, which extends both the rank invariant (also referred to as persistent Betti number), Puuska's rank invariant induced by epi-mono-preserving invariants of abelian categories, and the recently-defined persistent cup-length invariant, and we establish their stability. This generalized notion of persistent invariant also enables us to lift the Lyusternik-Schnirelmann (LS) category of topological spaces to a novel stable persistent invariant of filtrations, called the persistent LS-category invariant. See [Mémoli, Stefanou and Zhou, 2022] for our work.

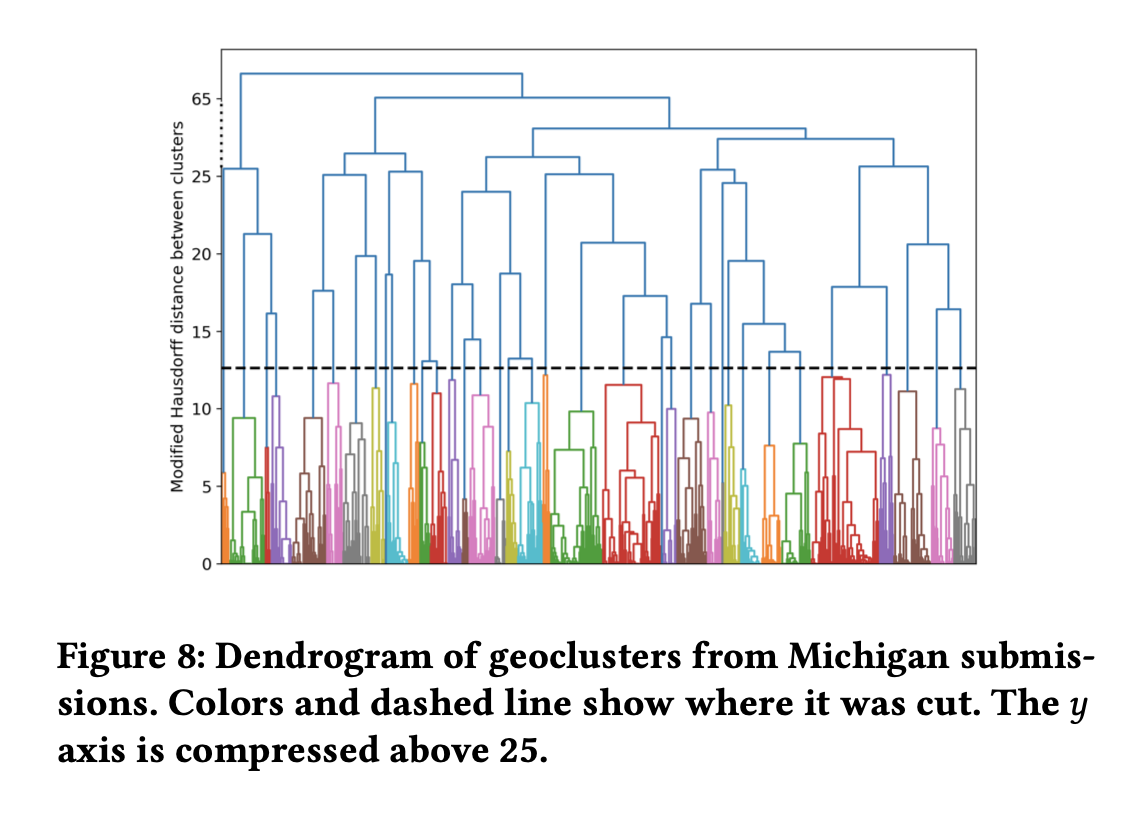
Aggregating community maps
This paper is motivated by a practical problem: many U.S. states have public hearings on "communities of interest" as part of their redistricting process, but no state has as yet adopted a concrete method of spatializing and aggregating community maps in order to take them into account in the drawing of new boundaries for electoral districts. Below, we describe a year-long project that collected and synthesized thousands of community maps through partnerships with grassroots organizations and/or government offices. The submissions were then aggregated by geographical clustering with a modified Hausdorff distance; then, the text from the narrative submissions was classified with semantic labels so that short runs of a Markov chain could be used to form semantic sub-clusters. The resulting dataset is publicly available, including the raw data of submitted community maps as well as post-processed community clusters and a scoring system for measuring how well districting plans respect the clusters. We provide a discussion of the strengths and weaknesses of this methodology and conclude with proposed directions for future work. See [Chambers, Duchin, Edmonds, Edwards, Matthews, Pizzimenti, Richardson, Rule and Stern, 2022] for our work.

Weisfeiler-Lehman meets Gromov-Wasserstein
The Weisfeiler-Lehman (WL) test is a classical procedure for graph isomorphism testing. The WL test has also been widely used both for designing graph kernels and for analyzing graph neural networks. In this paper, we propose the WeisfeilerLehman (WL) distance, a notion of distance between labeled measure Markov chains (LMMCs), of which labeled graphs are special cases. The WL distance is polynomial time computable and is also compatible with the WL test in the sense that the former is positive if and only if the WL test can distinguish the two involved graphs. The WL distance captures and compares subtle structures of the underlying LMMCs and, as a consequence of this, it is more discriminating than the distance between graphs used for defining the state-of-the-art Wasserstein Weisfeiler-Lehman graph kernel. Inspired by the structure of the WL distance we identify a neural network architecture on LMMCs which turns out to be universal w.r.t. continuous functions defined on the space of all LMMCs (which includes all graphs) endowed with the WL distance. Finally, the WL distance turns out to be stable w.r.t. a natural variant of the Gromov-Wasserstein (GW) distance for comparing metric Markov chains that we identify. Hence, the WL distance can also be construed as a polynomial time lower bound for the GW distance which is in general NP-hard to compute. See [Chen, Lim, Mémoli, Wan and Wang, 2022] for our work.

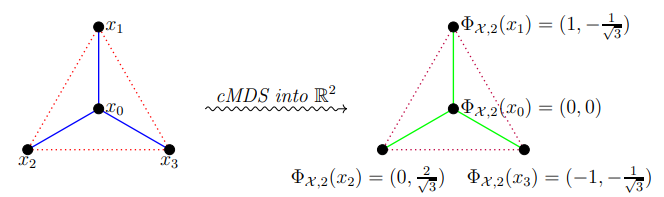
Classical MDS on Metric Measure Spaces
We generalize the classical Multidimensional Scaling procedure to the setting of general metric measure spaces. We develop a related spectral theory for the generalized cMDS operator, which provides a more natural and rigorous mathematical background for cMDS. Also, we show that the sum of all negative eigenvalues of the cMDS operator is a new invariant measuring non-flatness of a metric measure space. Furthermore, the cMDS output of several non-finite exemplar metric measures spaces, in particular the cMDS for spheres \(S^{d-1}\) and subsets of Euclidean space, are studied. Finally, we prove the stability of the generalized cMDS process with respect to the Gromov-Wasserstein distance. See [ Lim and Mémoli, 2022] for our work.

Diagrams of Persistence Modules Over Finite Posets
Starting with a persistence module - a functor M from a finite poset to the category of finite dimensional vector spaces - we seek to assign to M an invariant capturing meaningful information about the persistence module. This is often accomplished via applying a Mobius inversion to the rank function or birth-death function. In this paper we establish the relationship between the rank function and birth-death function by introducing a new invariant: the kernel function. The peristence diagram produced by the kernel function is equal to the diagram produced by the birth-death function off the diagonal and we prove a formula for converting between the persistence diagrams of the rank function and kernel function. See [Gulen and McCleary, 2022] for our work.

Some results about the Tight Span of spheres
The smallest hyperconvex metric space containing a given metric space X is called the tight span of X. It is known that tight spans have many nice geometric and topological properties, and they are gradually becoming a target of research of both the metric geometry community and the topological/geometric data analysis community. In this paper, we study the tight span of n-spheres (with either geodesic metric or l infinity-metric). See [Lim, Mémoli, Wan, Wang and Zhou, 2021] for our work.

Computing Generalized Rank Invariant for 2-Parameter Persistence Modules via Zigzag Persistence and its Applications
The notion of generalized rank invariant in the context of multiparameter persistence has become an important ingredient for defining interesting homological structures such as generalized persistence diagrams. Naturally, computing these rank invariants efficiently is a prelude to computing any of these derived structures efficiently. We show that the generalized rank over a finite interval I of a \(Z_2\)-indexed persistence module M is equal to the generalized rank of the zigzag module that is induced on a certain path in I tracing mostly its boundary. Hence, we can compute the generalized rank over I by computing the barcode of the zigzag module obtained by restricting the bifiltration inducing M to that path. If the bifiltration and I have at most t simplices and points respectively, this computation takes O(tω) time where ω∈[2,2.373) is the exponent of matrix multiplication. Among others, we apply this result to obtain an improved algorithm for the following problem. Given a bifiltration inducing a module M, determine whether M is interval decomposable and, if so, compute all intervals supporting its summands. See [Dey, Kim and Mémoli, 2021] for our work.

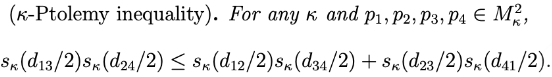
An interpretation of the 4-point condition of metric trees via Ptolemy's inequality
We identify a family of Ptolemaic inequalities in CAT(κ) spaces parametrized by κ and identify that the limit as κ→−∞ gives the 4-point condition of tree metric spaces. See [Gómez and Mémoli, 2021] for our work.

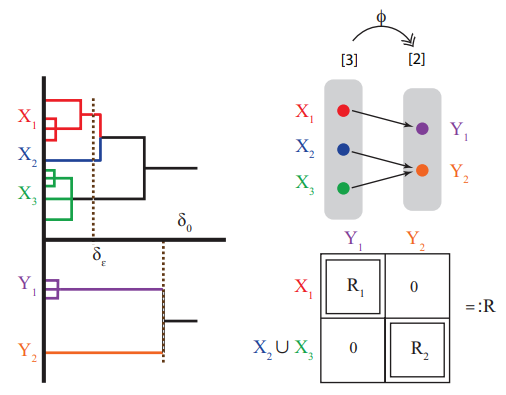
The Gromov-Hausdorff distance between ultrametric spaces: its structure and computation
The Gromov-Hausdorff distance (\(d_{GH}\)) provides a natural way of quantifying the dissimilarity between two given metric spaces. It is known that computing dGH between two finite metric spaces is NP-hard, even in the case of finite ultrametric spaces which are highly structured metric spaces in the sense that they satisfy the so-called \emph{strong triangle inequality}. Ultrametric spaces naturally arise in many applications such as hierarchical clustering, phylogenetics, genomics, and even linguistics. By exploiting the special structures of ultrametric spaces, (1) we identify a one parameter family \(\{d^{(p)}_{GH}\}_{p\in[1,\infty]}\) of distances defined in a flavor similar to the Gromov-Hausdorff distance on the collection of finite ultrametric spaces, and in particular \(d^{(1)}_{GH}=d_{GH}\). The extreme case when p=∞, which we also denote by uGH, turns out to be an ultrametric on the collection of ultrametric spaces. Whereas for all \(p\in[1,\infty)\), \(d^{(p)}_{GH}\) yields NP-hard problems, we prove that surprisingly \(u_{GH}\) can be computed in polynomial time. The proof is based on a structural theorem for uGH established in this paper; (2) inspired by the structural theorem for \(u_{GH}\), and by carefully leveraging properties of ultrametric spaces, we also establish a structural theorem for \(d_{GH}\) when restricted to ultrametric spaces. This structural theorem allows us to identify special families of ultrametric spaces on which \(d_{GH}\) is computationally tractable. These families are determined by properties related to the doubling constant of metric space. Based on these families, we devise a fixed-parameter tractable (FPT) algorithm for computing the exact value of \(d_{GH}\) between ultrametric spaces. We believe ours is the first such algorithm to be identified. See [ Mémoli, Smith and Wan, 2021] for our work.

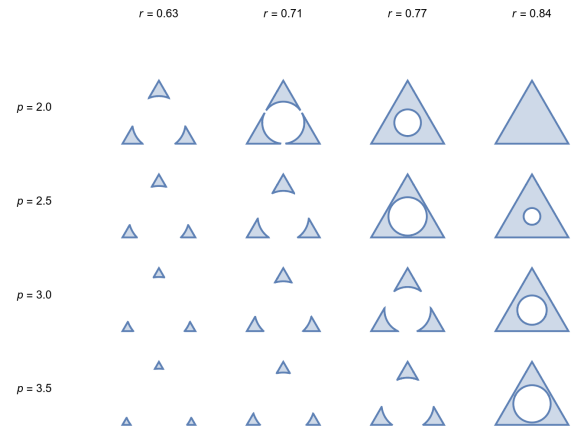
The Persistent Topology of Optimal Transport Based Metric Thickenings
A metric thickening of a given metric space X is any metric space admitting an isometric embedding of X. Thickenings have found use in applications of topology to data analysis, where one may approximate the shape of a dataset via the persistent homology of an increasing sequence of spaces. We introduce two new families of metric thickenings, the p-Vietoris-Rips and p-Čech metric thickenings for all 1≤p≤∞, which include all measures on X whose p-diameter or p-radius is bounded from above, equipped with an optimal transport metric. The p-diameter (resp. p-radius) of a measure is a certain ℓp relaxation of the usual notion of diameter (resp. radius) of a subset of a metric space. These families recover the previously studied Vietoris-Rips and Čech metric thickenings when p=∞. As our main contribution, we prove a stability theorem for the persistent homology of p-Vietoris-Rips and p-Čech metric thickenings, which is novel even in the case p=∞. In the specific case p=2, we prove a Hausmann-type theorem for thickenings of manifolds, and we derive the complete list of homotopy types of the 2-Vietoris-Rips thickenings of the n-sphere as the scale increases. See [ Adams, Mémoli, Moy and Wang, 2021] for our work.

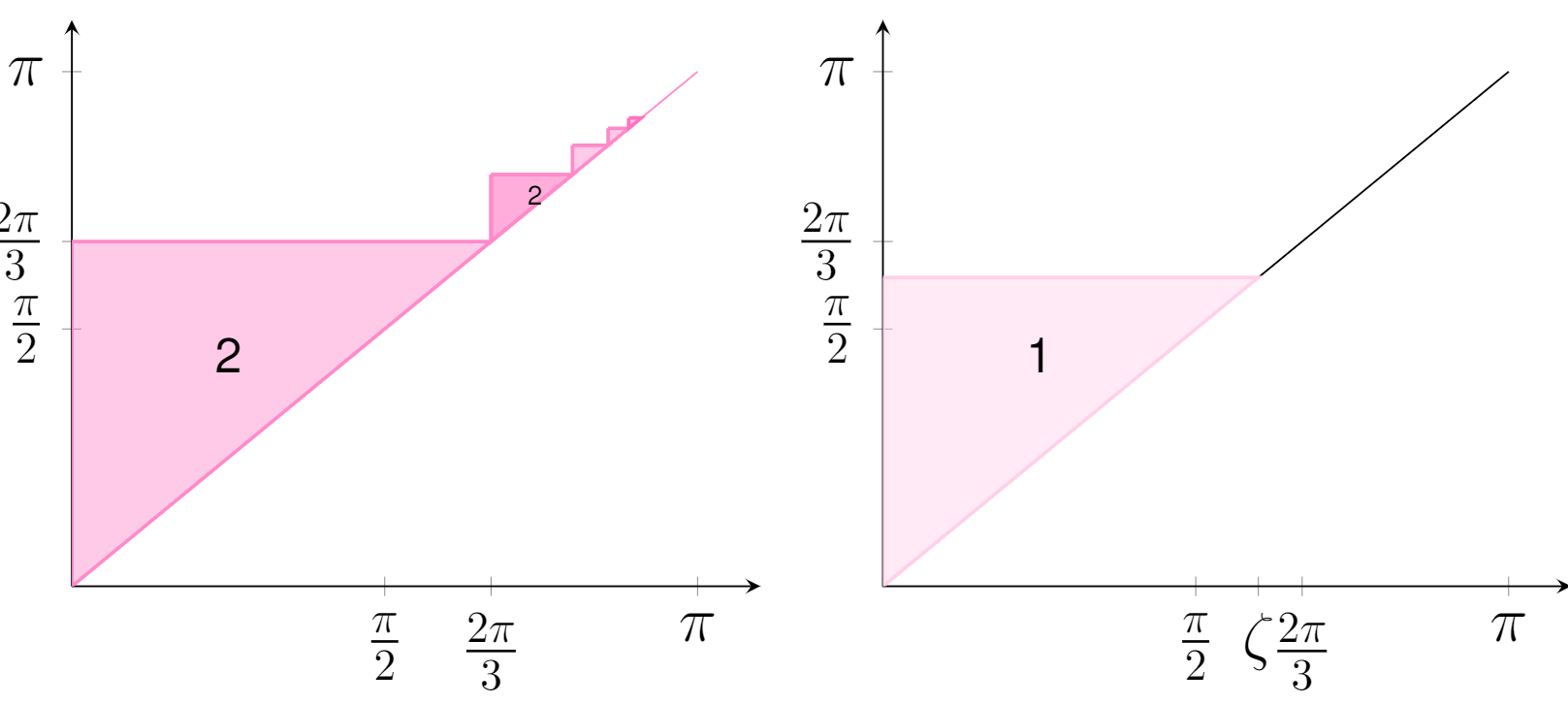
Persistent Cup-Length
We lift the cup-length into the Persistent Cup-Length invariant for the purpose of extracting non-trivial information about the evolution of the cohomology ring structure across a filtration. We show that the Persistent Cup-Length can be computed from a family of representative cocycles and devise a polynomial time algorithm for the computation of the Persistent Cup-Length invariant. We furthermore show that this invariant is stable under suitable interleaving-type distances. Along the way, we identify an invariant which we call the Cup-Length Diagram, which is stronger than persistent cup-length but can still be computed efficiently. Read more in [Contessoto, Mémoli, Stefanou and Zhou, 2021].

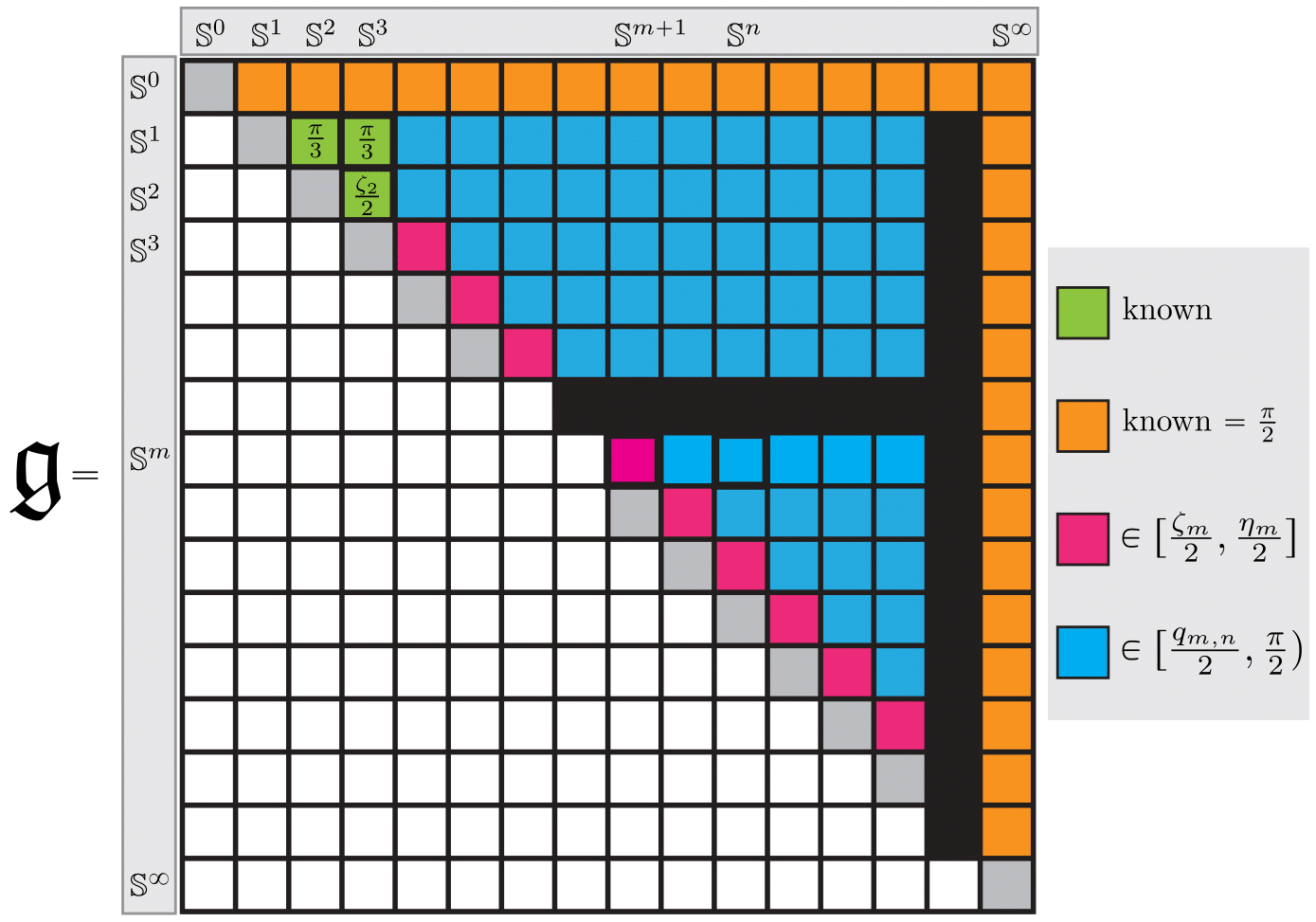
The Gromov-Hausdorff distance between spheres
We provide general upper and lower bounds for the Gromov-Hausdorff distance between m-sphere and n-sphere (endowed with the round metric) for m and n between zero and infinity. Some of these lower bounds are based on certain topological ideas related to the Borsuk-Ulam theorem. Via explicit constructions of (optimal) correspondences we prove that our lower bounds are tight in some cases. We also formulate a number of open questions. Read more in [Lim, Mémoli and Smith, 2021].

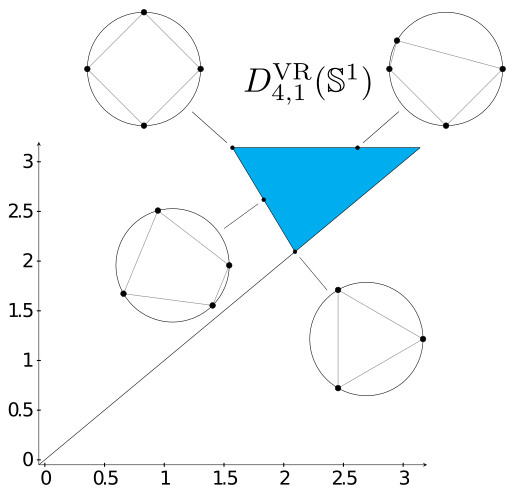
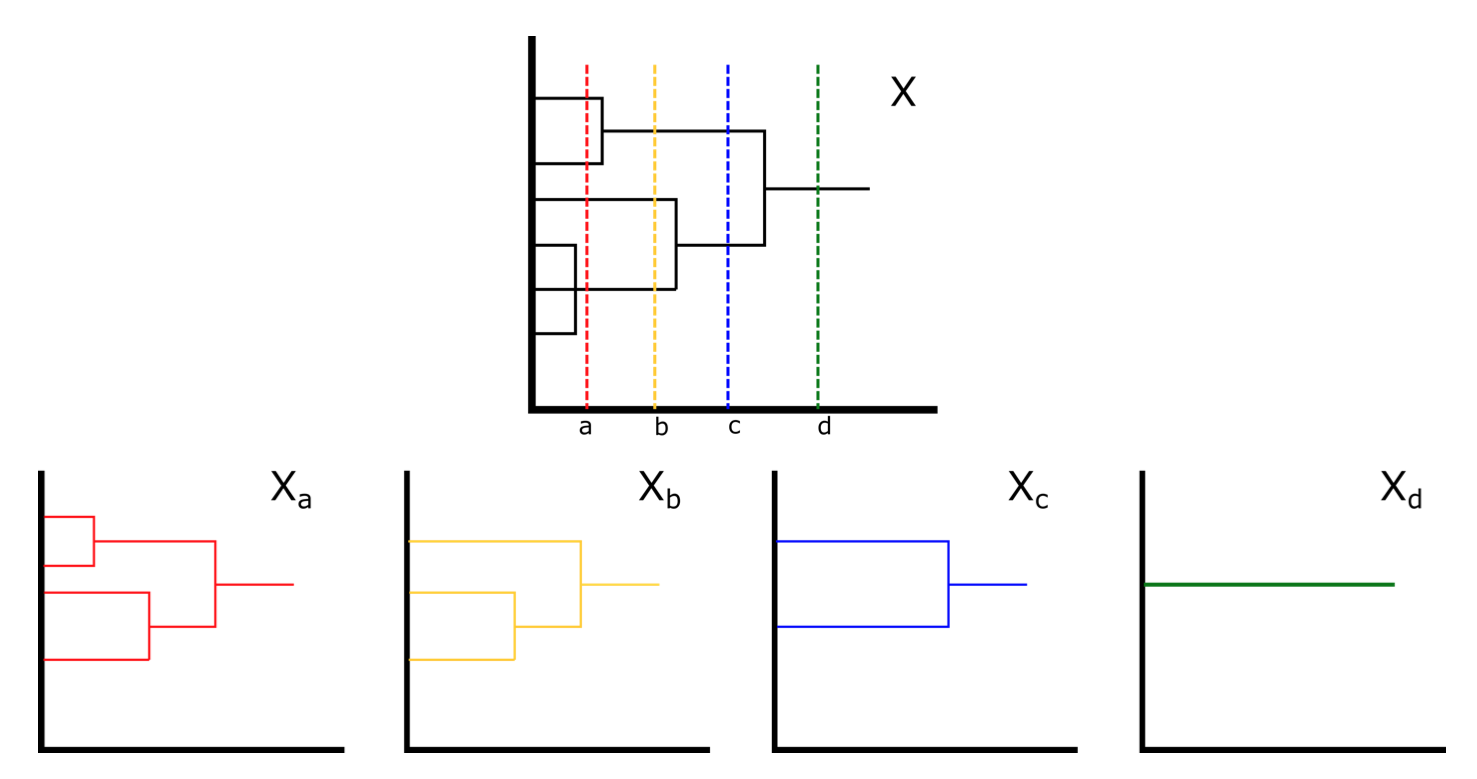
Curvature sets over persistence diagrams
Inspired by Gromov's idea of the curvature sets, we define the (n,k)-Persistence Set of a compact metric space M as the collection of k-dimensional persistence diagrams of all samples X with n points. When M is finite, Persistence Sets provide a computationally cheaper alternative to the Vietoris-Rips complex of M, as the boundary matrices are significantly smaller whenever n<<|M|. In the special case that n=2k+2, it can be shown that the Vietoris-Rips persistent homology of X only has one interval in dimension k. This allows us to visuallize the (2k+2,k)-Persistence Set by overlaying the diagrams of all samples X into one set of axes. The image on the side shows the (4,1)-Persistence Set of the unit circle equipped with the shortest path distance. The configurations shown point to their respective persistence diagram inside of the Persistence Set. These invariants can detect the homotopy type of a certain family of metric graphs. [Gómez and Mémoli, 2021]

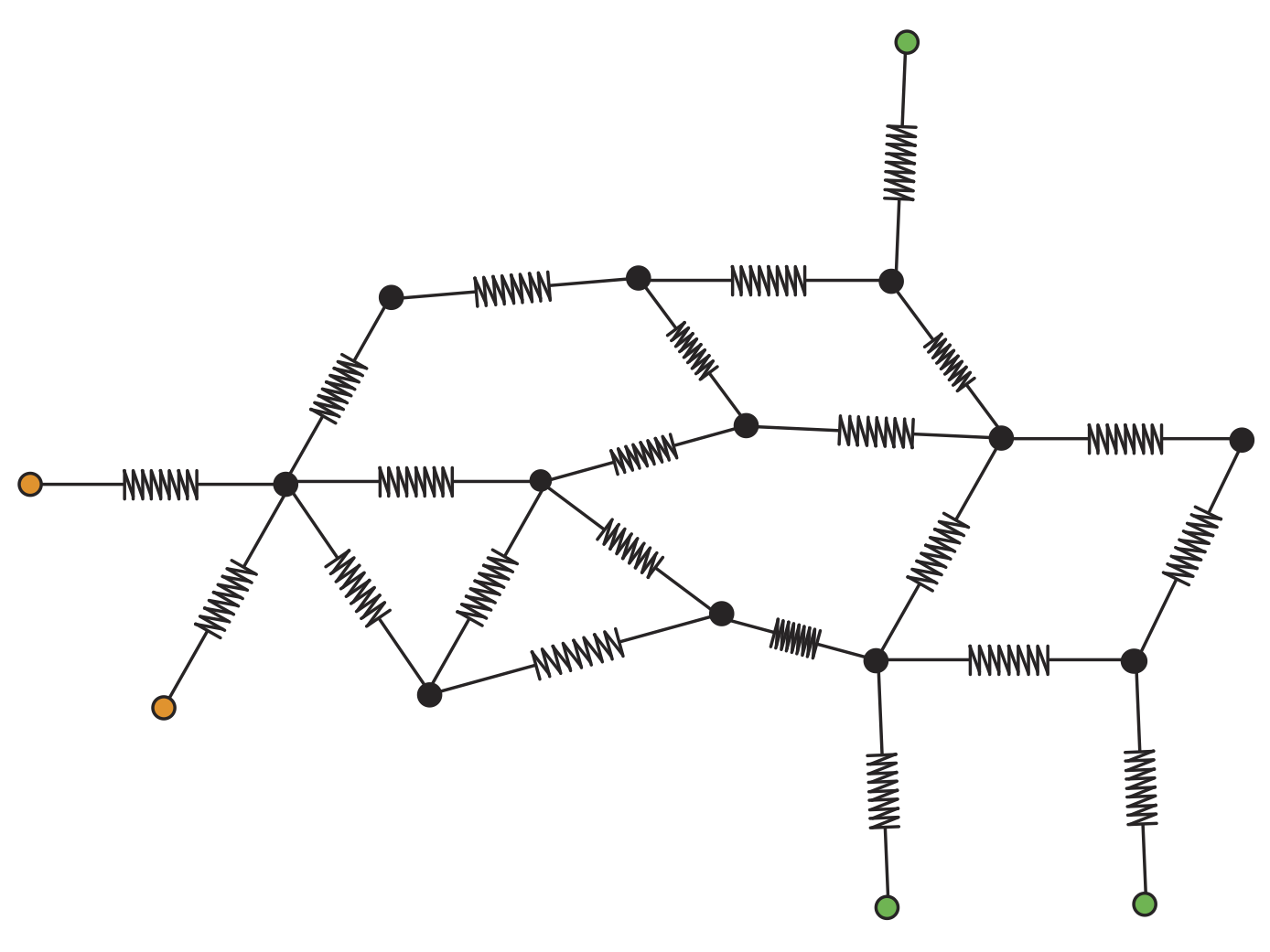
Persistent Laplacians
In this work we present a thorough study of the theoretical properties and devise efficient algorithms for the persistent Laplacian, an extension of the standard combinatorial Laplacian to the setting of simplicial pairs: pairs of simplicial complexes related by an inclusion, which was recently introduced by Wang et al. in [1]. In analogy with the non-persistent case, we establish that the nullity of the q-th persistent Laplacian equals the q-th persistent Betti number of any given simplicial pair which provides an interesting connection between spectral graph theory and TDA. We further exhibit a novel relationship between the persistent Laplacian and the notion of Schur complement of a matrix. This relation permits us to uncover a link with the notion of effective resistance from network circuit theory and leads to a persistent version of the Cheeger inequality. This relationship also leads to a novel and fundamentally different algorithm for computing the persistent Betti number for a pair of simplicial complexes which can be significantly more efficient than standard algorithms. See [ Mémoli, Wan and Wang, 2020] for our work.

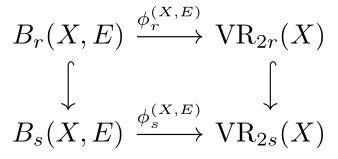
Vietoris-Rips Persistent Homology, Injective Metric Spaces, and The Filling Radius
In the applied algebraic topology community, the persistent homology induced by the Vietoris-Rips simplicial filtration is a standard method for capturing topological information from metric spaces. In this paper, we consider a different, more geometric way of generating persistent homology of metric spaces which arises by first embedding a given metric space into a larger space and then considering thickenings of the original space inside this ambient metric space. In the course of doing this, we construct an appropriate category for studying this notion of persistent homology and show that, in a category theoretic sense, the standard persistent homology of the Vietoris-Rips filtration is isomorphic to our geometric persistent homology provided that the ambient metric space satisfies a property called injectivity. Read more in [Lim, Mémoli and Okutan, 2020]

Elder-Rule-Staircodes for Augmented Metric Spaces
An augmented metric space \((X, d_X, f_X)\) is a metric space \((X, d_X)\) equipped with a function \(f_X: X \to \mathbb{R}\). It arises commonly in practice, e.g, a point cloud \(X\) in \(\mathbb{R}^d\) where each point \(x\in X\) has a density function value \(f_X(x)\) associated to it. Such an augmented metric space naturally gives rise to a 2-parameter filtration \(\mathcal{K}\). However, the resulting 2-parameter persistence module \(H_0(\mathcal{K})\) could still be of wild representation type, and may not have simple indecomposables. Motivated by the elder-rule for the zeroth homology of a 1-parameter filtration, we propose a barcode-like summary, called the elder-rule-staircode, as a way to encode \(H_0(\mathcal{K})\). Specifically, given a finite \((X, d_X, f_X)\), its elder-rule-staircode consists of \(n = |X|\) number of staircase-like blocks in the plane. We show that if \(H_0(\mathcal{K})\) is interval decomposable, then the barcode of \(H_0(\mathcal{K})\) is equal to the elder-rule-staircode. Furthermore, regardless of the interval decomposability, the fibered barcode, the dimension function (a.k.a. the Hilbert function), and the graded Betti numbers of \(H_0(\mathcal{K})\) can all be efficiently computed once the elder-rule-staircode is given. Finally, we develop and implement an efficient algorithm to compute the elder-rule-staircode in \(O(n^2\log n)\) time, which can be improved to \(O(n^2\alpha(n))\) if \(X\) is from a fixed dimensional Euclidean space \(\mathbb{R}^d\), where \(\alpha(n)\) is the inverse Ackermann function. [ Proceedings of the 36th International Symposium on Computational Geometry (SoCG 2020) ]

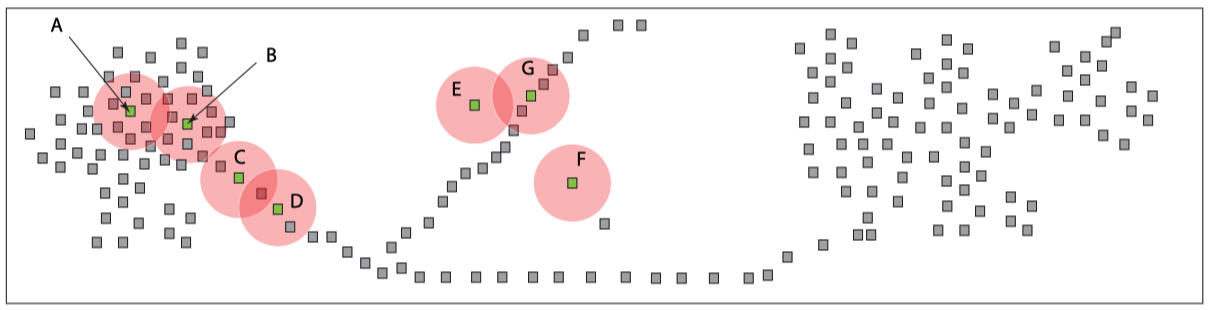
The Wasserstein transform
We introduce the Wasserstein transform (WT), a family of methods for enhancing and denoising datasets defined on general metric spaces. The construction draws inspiration from Optimal Transportation ideas and also connects with the mean shift family of algorithms. We exhibit the usefulness of WT in ameliorating the chaining effect, a well-known obstacle for clustering tasks and also other application scenarios such as image classification, image segmentation and NLP. See [Mémoli, Smith and Wan, 2019 ] and [Jin, Mémoli and Wan, 2020] for our work on the topic.

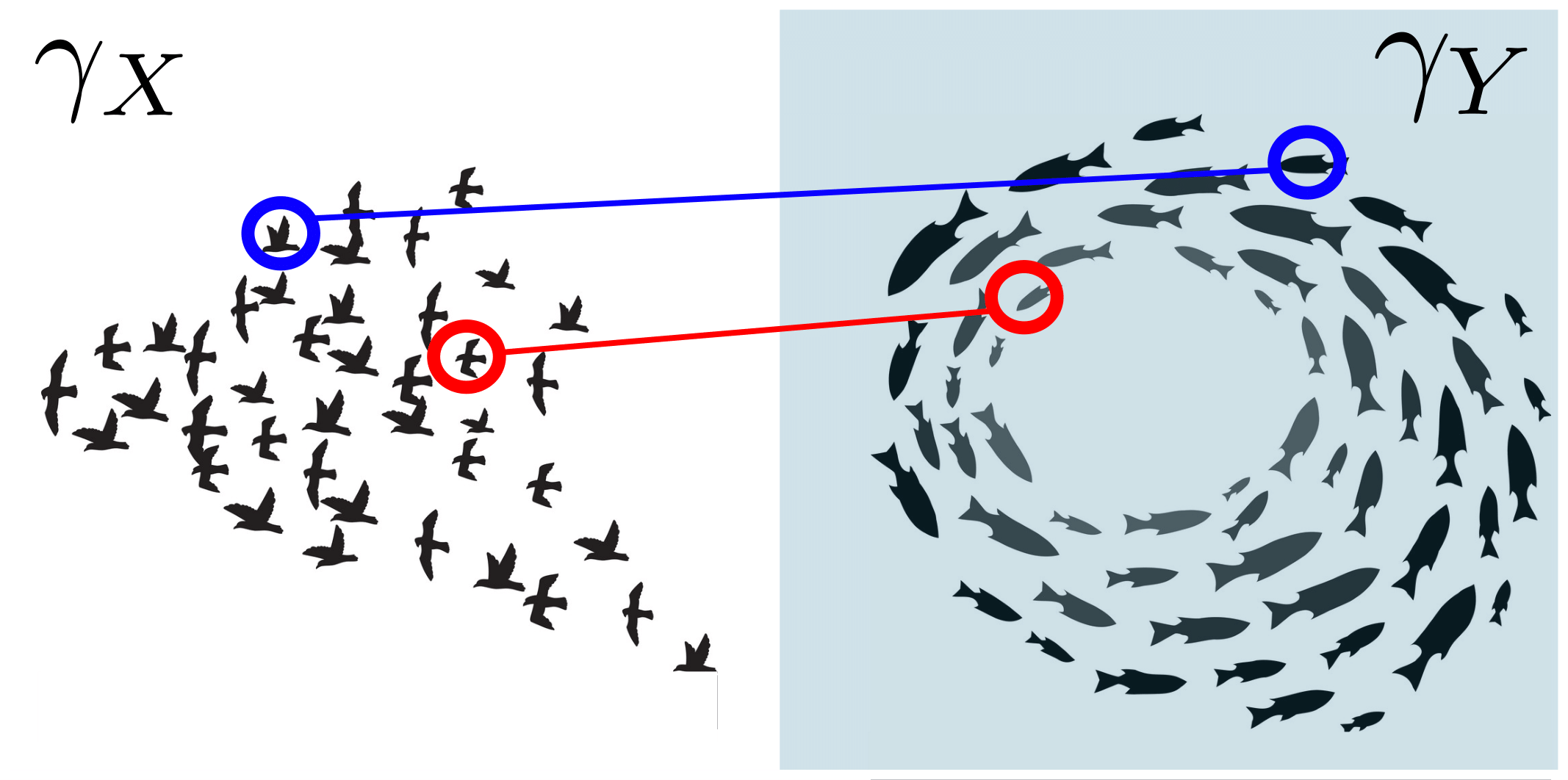
Spatiotemporal Persistent Homology for Dynamic Metric Spaces
Characterizing the dynamics of time-evolving data within the framework of topological data analysis (TDA) has been attracting increasingly more attention. Popular instances of time-evolving data include flocking/swarming behaviors in animals and social networks in the human sphere. A natural mathematical model for such collective behaviors is a dynamic point cloud, or more generally a dynamic metric space (DMS). In this paper we extend the Rips filtration stability result for (static) metric spaces to the setting of DMSs. We do this by devising a certain three-parameter “spatiotemporal” filtration of a DMS. Applying the homology functor to this filtration gives rise to multidimensional persistence module derived from the DMS. We show that this multidimensional module enjoys stability under a suitable generalization of the Gromov–Hausdorff distance which permits metrization of the collection of all DMSs. On the other hand, it is recognized that, in general, comparing two multidimensional persistence modules leads to intractable computational problems. For the purpose of practical comparison of DMSs, we focus on both the rank invariant or the dimension function of the multidimensional persistence module that is derived from a DMS. We specifically propose to utilize a certain metric d for comparing these invariants: In our work this d is either (1) a certain generalization of the erosion distance by Patel, or (2) a specialized version of the well-known interleaving distance. In either case, the metric d can be computed in polynomial time. [Discrete & Computational Geometry 2020]

Persistent Homotopy Groups of Metric Spaces
With the aim of enlarging the toolset of persistence theory, which has traditionally dealt with homology groups and their persistent versions, we study notions of persistent homotopy groups of compact metric spaces together with their stability properties in the Gromov-Hausdorff sense. We pay particular attention to the case of persistent fundamental groups for which we obtain a more precise description. Under fairly mild assumptions on the spaces, the classical fundamental group, isomorphic to the limit of the persistent fundamental group, has an underlying tree-like structure (i.e. a dendrogram) and an associated ultrametric. See [Mémoli and Zhou, 2019].

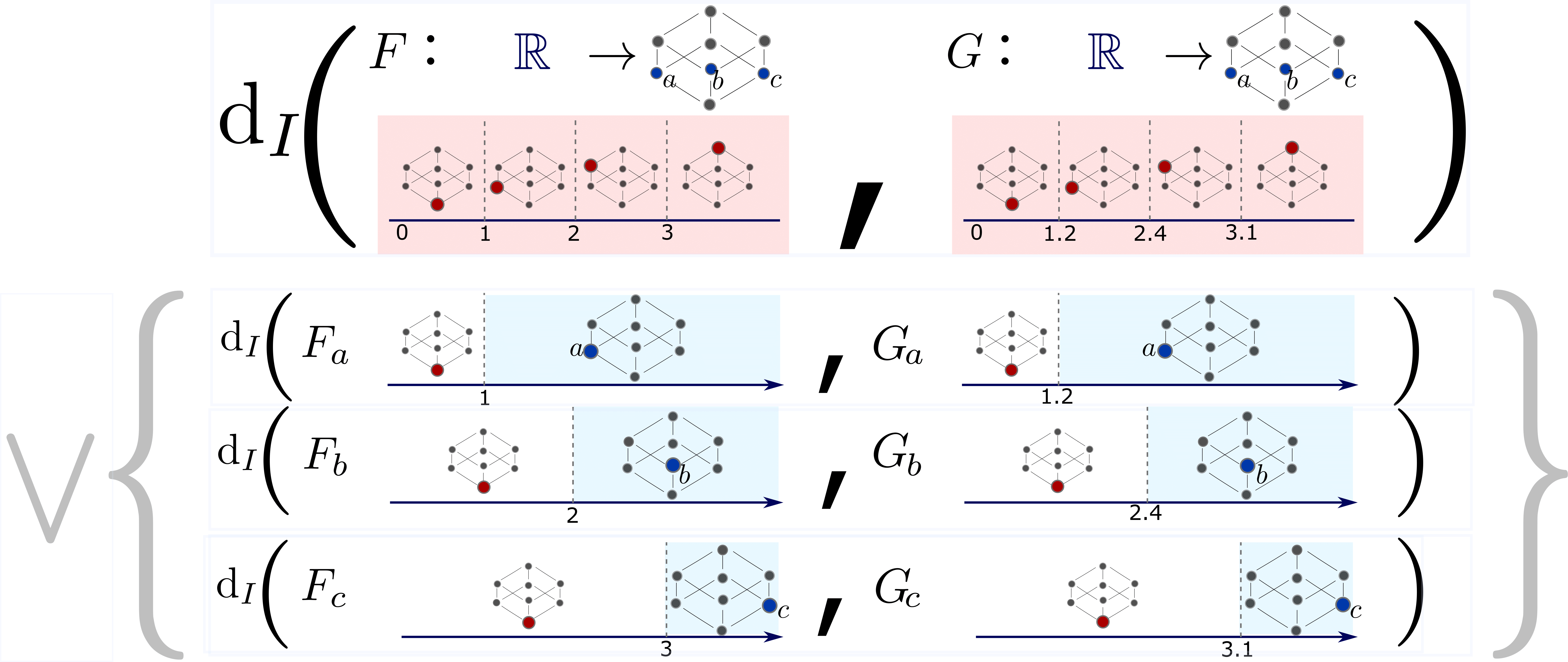
Interleaving by Parts for Persistence In a Poset
Metrics in computational topology are often either (i) themselves in the form of the interleaving distance d(F,G) between certain order-preserving maps F and G between posets or (ii) admit d(F,G) as a tractable lower bound. Assuming that the target poset of F and G admits a join-dense subset, we propose certain join decompositions of F and G which facilitate the computation of d(F,G). We leverage this result in order to (i) elucidate the structure and computational complexity of the interleaving distance for poset-indexed clusterings (i.e. poset-indexed subpartition-valued functors), (ii) to clarify the relationship between the erosion distance by Patel and the graded rank function by Betthauser, Bubenik, and Edwards, and (iii) to reformulate and generalize the tripod distance by the second author.[Kim, Mémoli and Stefanou, 2019]

Computing Gromov-Hausdorff distances between ultrametric spaces
In recent years, the Gromov-Hausdorff distance has been widely used for shape analysis and for establishing stability results for topological invariants in TDA. However, the distance is well-known to be NP-hard to compute, even when restricted to ultrametric spaces. Ultrametric spaces naturally arise in many application areas such as hierarchical clustering, phylogenetics, genomics, and even linguistics. In this project, we (1) found a polynomial-time computable variant of the Gromov-Hausdorff distance on the collection of ultrametric spaces, and (2) identified subcollections of ultrametric space on which the Gromov-Hausdorff distance can be computed in polynomial time. See [Mémoli, Smith and Wan, 2019] for details. We also extend our study of Gromov-Hausdorff distance to ultrametric measure spaces and consider applications to phylogenetic trees; see [Mémoli, Munk, Wan and Weitkamp, 2021] for details.

Network metrics
A natural question to ask when comparing two networks is: are these networks the same, or are they different? The difference between two networks can be formally quantified by developing metrics on the collections of all networks. Understanding the behavior of such metrics is one of our ongoing projects. See the related papers [Chowdhury and Mémoli, 2017], [Chowdhury and Mémoli, 2018], and [Chowdhury and Mémoli, 2018].

Clustering networks
Clustering methods, in particular hierarchical clustering methods, can be very useful in exploratory data analysis. Classical hierarchical clustering reveals the presence of clusters across a range of scales for metric datasets (i.e. "well-behaved" datasets), from which researchers are often able to find hidden groupings and patterns. However, general network data tends to be more "wild." We are interested in being able to provide hierachical clustering schemes that simplify the visualization of even very general network data, while providing theoretical guarantees on the worst-case distortion that can occur from applying such clustering methods. See [Chowdhury, Mémoli and Smith, 2016] and [Smith, Chowdhury and Mémoli, 2016].

Persistent Homology of Networks
An ongoing project in our group is to better understand the persistent homology of a general network. In addition to devising robust theoretical methods for producing persistence diagrams from networks, we are interested in using our methods to glean new insights into the structures of a wide range of network datasets. See the related works [Chowdhury and Mémoli, 2018], [Czumaj, 2018], and [Poster].

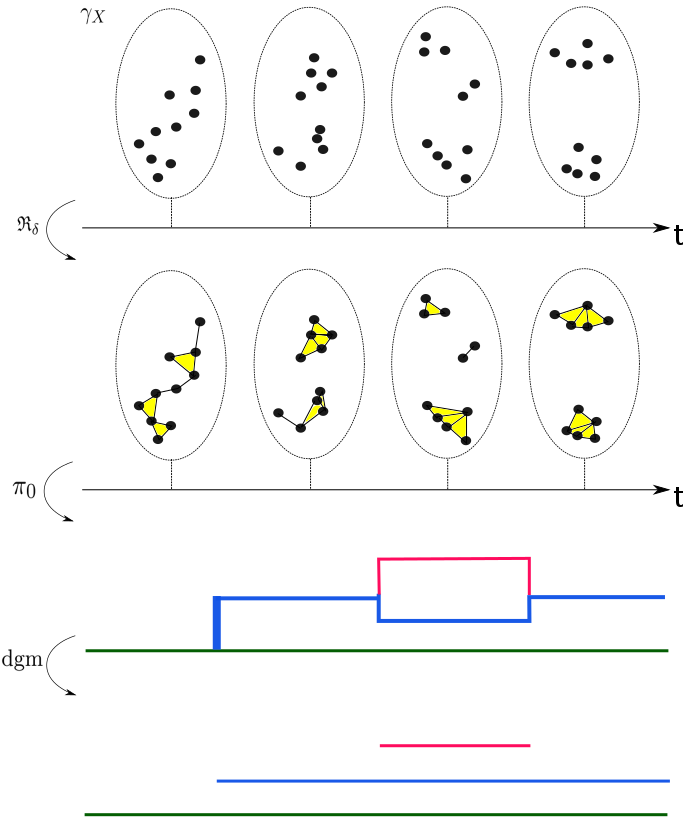
Zigzag Persistent Homology of Dynamic Networks
When studying flocking/swarming behaviors in animals one is interested in quantifying and comparing the dynamics of the clustering induced by the coalescence and disbanding of animals in different groups. Motivated by this, we study the problem of obtaining persistent homology based summaries of time-dependent metric data. Our research has produced the notions of formigrams, and distances between dynamic metric spaces, and dynamic graphs. Fot the interphase with the data anlysis part, we use concepts from zigzag persistent homology. Read more in https://research.math.osu.edu/networks/formigrams/. See https://research.math.osu.edu/networks/formigramator/ for an interatctive demo which can compute formigrams of user specified data.

Zigzag Persistent Homology for Neural Data
We apply Zigzag Persistent Homology towards understanding the amount of information contained in the spike trains of hippocampal place cells. Previous work has established that simply knowing which groups of place cells fire together in an animal's hippocampus is sufficient to extract the global topology of the animal's physical environment. We model a system where collections of place cells group and ungroup according to short-term plasticity rules. We obtain the surprising result that in experiments with spurious firing, the accuracy of the extracted topological information decreases with the persistence (beyond a certain regime) of the cell groups. This suggests that synaptic transience, or forgetting, is a mechanism by which the brain counteracts the effects of spurious place cell activity. PLoS ONE link.

Metric graph approximation of geodesic spaces
A standard result in metric geometry is that every compact geodesic metric space can be approximated arbitrarily well by finite metric graphs in the Gromov-Hausdorff sense. It is well known that the first Betti number of the approximating graphs may blow up as the approximation gets finer. In our work, given a compact geodesic metric \(X\), we define a sequence \((\delta^X_n)_{n \geq 0}\) of non-negative real numbers by $$\delta^X_n:=\inf \{d_{GH}(X,G): G \text{ a finite metric graph, } \beta_1(G)\leq n \} .$$ By construction, and the above result, this is a non-increasing sequence with limit \(0\). We study this sequence and its rates of decay with \(n\). We also identify a precise relationship between the sequence and the first Vietoris-Rips persistence barcode of \(X\). Furthermore, we specifically analyze \(\delta_0^X\) and find upper and lower bounds based on hyperbolicity and other metric invariants. As a consequence of the tools we develop, our work also provides a Gromov-Hausdorff stability result for the Reeb construction on geodesic metric spaces with respect to the function given by distance to a reference point. [Mémoli and Okutan, 2018].

Optimal Transport and Persistent Homology based distances between shapes
Our group has studied different methods for discriminating shapes. In many cases we see shapes/datasets as metric spaces or metric-measure spaces and utilize either the Gromov-Hausdorff or the Gromov-Wasserstein distance as bases for our studies. These distances admit several poly-time computable lower bounds which can be used in practical applications. For instance, given a metric measure space \((X,d_X,\mu_X)\) one can consider the so called local shape distribution \(h_X(x,t):=\mu_X(\overline(B_t(x)))\) as a feature of the space \(X\). Now, given two such spaces on sets up an optimal transport problem involving both \(h_X\) and \(h_Y\) whose solution turns out to be a lower bound for the Gromov-Wasserstein distance. See this paper and Ying Yin's MMS CPS thesis work demo.